- 英고액권 50파운드 초상 인물
- 컴퓨터 빼닮은 ‘튜링머신’ 제시
- ‘정지문제’는 계산 불가능 증명
- 구 소련 수학자 페일러와 레만
- 그래프 동형문제 연구 큰 성과
- ‘신경학습’ 주된 방법론에 기여
- 수학서 출발한 AI·컴퓨터과학
- 독립 후엔 상호작용으로 발전
 |
| 앨런 튜링의 사진이 담긴 영국 50파운드 지폐. 튜링은 인공지능(AI)컴퓨터(오른쪽 사진)의 기본 개념을 수립했을 뿐만 아니라 2차 세대대전 당시 24시간마다 바뀌는 독일군의 ‘애니그마’ 암호를 풀어내 노르망디 상륙작전의 성공에 지대한 공을 세웠다는 평가를 받고 있다. 국제신문 DB |
■인공지능의 수학적 기원
19세기 후반부터 수학계에서는 수학의 기초 토대를 마련하기 위해 여러 관점이 제시됐다. 칸토어는 수학의 근간이 되는 집합론을 창시해 무한의 개념을 엄밀하게 다루게 되었으나 러셀의 파라독스가 제기됨으로써 집합론으로부터 시작되는 수학의 체계에 관한 근본 논의가 시작됐다. 논리주의 직관주의 형식주의가 대표적이다. 논리주의는 수학을 논리학의 일부로 치환하려는 노력이었고, 직관주의는 수학이 인간 정신활동의 산물로, 직관적으로 혹은 본능적으로 참으로 여겨지는 명제만이 참인 것으로 인식된다. 마지막으로 형식주의는 수학이 몇 가지 공리로부터 출발해 기호의 기계적인 연역을 통해 체계를 완성할 수 있다는 주장이다.
형식주의 대표적인 옹호자인 독일의 수학자 힐버트(David Hilbert)는 1928년 세계수학자대회(ICM·International Congress of Mathematics)에서 완벽성(Completeness) 무모순성(Consistence) 결정성(Decidability)이 담보되는 수학의 공리체계가 존재할 것이라고 주장했다. 이를 ‘힐버트 프로그램’이라고 한다. 간략히 설명하면, 완벽성은 “모든 참인 명제는 공리로부터 도출될 수 있다”이고, 무모순성은 “공리체계가 모순이 없음은 주어진 공리계 안에서 증명될 수 있다”이며, 결정성은 “항상 명제의 참과 거짓을 결정할 수 있는 알고리즘이 있다”는 것으로 결정문제(Entscheidungsproblem)로 불리운다. 그러나 불행히도 몇 해 지나지 않아 힐버트가 제시한 세 가지 원칙은 모두 가능하지 않음이 증명된다.
먼저, 괴델(Kurt Godel)은 불완전성 정리를 증명해 완벽성과 무모순성이 성립하지 않음을 보였다. 괴델의 불완전성 정리는 그 당시 수학계의 화두였다. 당시 수학의 중심이었던 유럽 유수한 대학의 수학과에서는 괴델의 정리에 관한 강의가 개설되었는데, 영국 케임브리지 대학의 수학자 앨런 튜링(Alan Turing)은 자신만의 독특한 방법으로 힐버트의 결정문제에 관한 해답을 제시했다. 튜링은 ‘튜링머신’이라는 가상의 기계를 고안해, 결정문제에 등장하는 ‘알고리즘’을 이 기계가 계산할 수 있다는 것으로 규정했다. 그는 소위 ‘정지문제(Halting problem)’라는 것은 튜링머신으로 계산될 수 없음을 증명함으로써 힐버트의 결정문제를 풀었다.
튜링머신은 입력할 숫자들을 적을 수 있는 테이프, 이들 숫자를 읽거나 쓸 수 있는 ‘헤드’, 이들의 작동규칙을 결정하는 ‘제어기’ 등 세 가지 구성요소를 가지고 있다. 놀랍게도 이런 각각의 구성요소는 현대컴퓨터에 메모리, 중앙처리장치(CPU) 및 키보드, 모니터와 같은 입출력 장치로 고스란히 재현되고 있다. 이후 튜링은 기계가 계산할 수 있는 것, 즉 기계지능에 관한 연구를 계속해 ‘이미테이션 게임(튜링테스트)’ 같은 인공지능(AI) 연구에 막대한 영향을 끼쳤다. 영란은행은 2019년 새로운 50파운드 지폐의 초상 인물로 튜링을 선정, 그의 업적을 기리고 있다.
 |
| 튜링머신을 물리적으로 구현한 모델. 영문 위키피디아 |
■그래프 신경학습과 동형문제
위에서 언급된 서방세계의 앨런 튜링이나 마빈 빈스키, 존 매카시 등이 인공지능 연구의 시초로 여겨지고 있으나, 소련의 인공지능 초기 연구는 알려지지 않았다. 1960년대의 컴퓨터과학의 주요 연구주제 중 하나는 알고리즘의 계산복잡도였다. 즉, 빠른 알고리즘과 그렇지 않은 알고리즘으로 구분하는 연구였다. 다양한 문제가 분류되고 있었으나 실질적으로 중요한 문제였던 그래프 동형문제에 관해서는 빠른 알고리즘이 알려지지 않았다. 그래프는 점과 이를 연결한 선을 추상화한 수학적인 개념인데, 그래프 동형문제란 주어진 두 그래프가 같은 그래프인지를 판별하는 문제다.
당시 소련의 AI 연구소의 젊은 수학자인 바이스 페일러(Boris Weisfeiler)와 레만(Andrey Leman)은 두 그래프가 동형일 필요조건을 계산 가능한 빠른 알고리즘으로 구현했다.
지금은 ‘Weisfeiler-Leman algorithm’으로 불리고 있다. 이 알고리즘은 주어진 그래프의 각각의 점에서 주변의 연결된 점의 정보를 취합하는 과정을 통해 그래프 특성을 파악하는 게 핵심이다. 이런 그래프의 각 점에서 주변의 정보를 취합하고 자신의 정보와 결합하는 ‘Aggregate-Combine’ 방법은 현대 그래프 신경학습의 주된 방법론인 ‘Massage Passing’에 그대로 적용되고 있다.
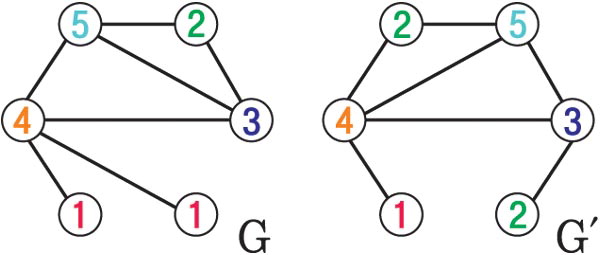 |
| 주어진 두 개의 그래프 G, G’
출처:Weisfeiler-Lehman Graph Kernels(2011, N. Shervashidze et al) |
■수학과 인공지능 연구의 상호 작용
위에서 언급된 바와 같이 최근 딥러닝을 비롯한 인공지능 알고리즘의 초기 연구는 수학의 한 분야였고, 현재도 수학적 원리나 개념을 기반으로 연구되고 있다.
알고리즘이란 용어도 수학에서 출발했고 알고리즘에서 기본적인 서술은 수학적인 기호나 용어로 기술된다. 이렇게 인공지능이나 컴퓨터과학은 수학에서 출발했으나 이후 수학과는 별개로 독립된 연구 분야로 자리매김 했으며 수학과 지속적인 상호작용으로 발전하고 있다.
최근에는 전통적으로 자연과학이나 공학에 널리 활용되는 선형대수학 미적분학 확률론 등의 분야뿐 아니라 수학의 세분된 전문분야인 (편)미분방정식 미분기하 위상수학 등의 순수수학으로 분류되던 수학의 영역까지도 활용돼 딥러닝이나 머신러닝 알고리즘에 적용되고 있다. 또한 반대로 이렇게 개발된 인공지능 알고리즘을 활용해 전통적인 수학 문제를 해결하거나 새로운 수학적 명제를 발견하는 데 도움을 주고 있다.
# 수리연 기하학 활용, 그래프신경망 연구
 |
| 기하적 딥러닝의 대상.
출처:‘Geometric Deep Learning Grids, Groups, Graphs, Geodesics, and Gauges’ by Bronstein et al. |
19세기 후반 독일의 수학자 클라인(Felix Klein)은 전통적인 유클리드 기하와 18, 19세기를 거쳐 발전되어온 여러 비유클리드 기하를 통합해 기하학의 현대적 의미를 부여했다. 엘랑겐 프로그램(Erlangen program)이라고 말하는 것으로, 클라인은 기하학의 중요한 관점을 대수적인 개념인 군(群) 이론을 활용해 기하적인 대상의 변환불변량에 두어야 한다고 주장했다. 이런 기하학에 관한 관점은 현대적 개념의 기하학에 근간을 이뤄 위상수학 미분기하 대수기학 발전에 초석을 마련했다. 또한 수학뿐만 아니라 에너지의 보존법칙과 대칭성의 관계를 설명하는 뇌터의 정리(Noether’s theorem)를 통해 현대물리학에도 큰 영향을 주었다.
최근 데이터과학의 기계학습 분야에서도 비슷한 시도가 이루어지고 있다. RNN(순환신경망) CNN(합성곱신경망) GNN(그래프신경망) 등의 다양하게 개발된 많은 종류의 기계학습 원리를 기하학의 관점에서 접근해 통합적인 해석을 하려는 움직임이다. 소위 ‘기하적 딥러닝(Geometric deep learning)’이라고 한다.
국가수리과학연구소 응용기하팀은 이런 연구주제 가운데 하나인 그래프 표현론 및 그래프신경망 연구를 진행하고 있다. 현실의 데이터는 엑셀데이터와 같이 숫자의 정형적 구조뿐만 아니라 기하학적인 구조를 가진 그래프나 다양체로 표현되는 경우가 많다. 소셜네트워크 논문네트워크(citation network) 교통망 뇌신경망지도 분자구조 등이 대표적인 예라고 할 수 있다. 연구소는 이런 데이터의 분석을 전통적인 기계학습 방법론을 넘어 위상수학, 기하학 등 심화된 수학 연구와 접목해 기존 인공지능 알고리즘 개선, 기하적 특성을 보존하는 표현학습 알고리즘 개발 및 안정성 증명으로 알고리즘의 신뢰성을 확보하고자 노력하고 있다.
※공동기획:국제신문·국가수리과학연구소







